1 次 方程式 解き方 219656

3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ
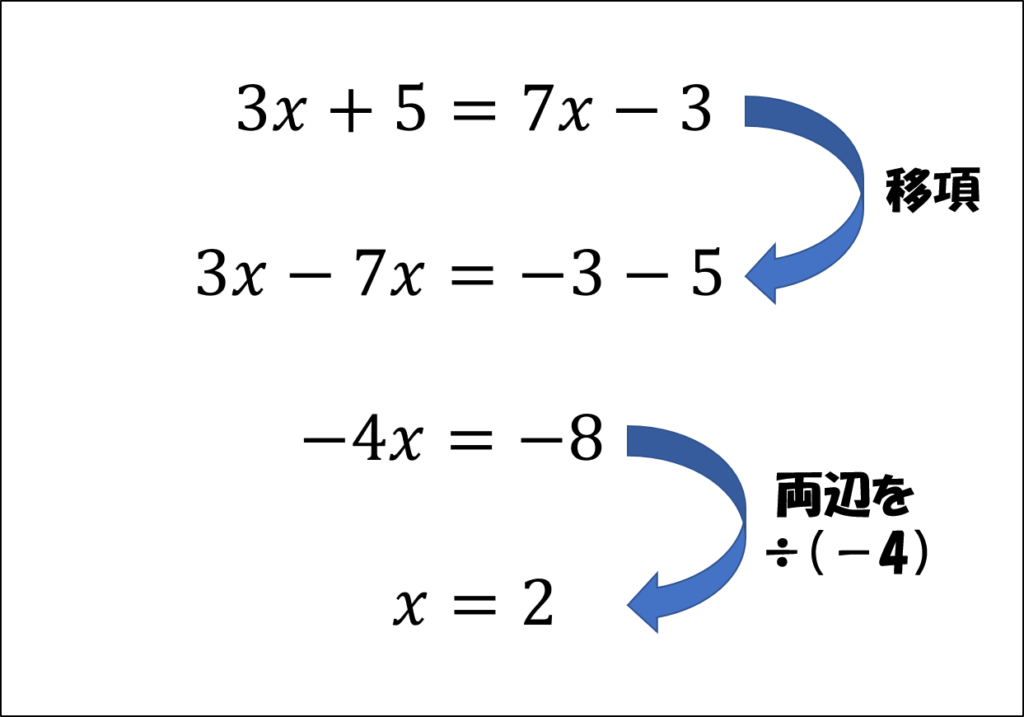
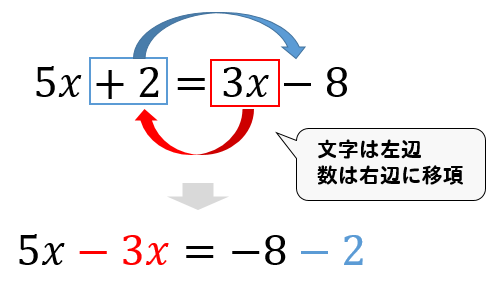
方程式の解き方の手順 ①文字の項をイコールの左側に数字だけの項をイコールの右側に集める。(移行) ②集めた物を計算する。 ③文字の係数の逆数をかける。 方程式はこの3工程で解答まで導くことができます。 中学1年生の初めの壁です。しっかりと理解して乗り越えていきましょう1次方程式の解き方① 1次方程式の解き方② 文字式と方程式の区別 比例・反比例の文章題 資料の整理 等式変形 連立方程式の文章題(池) 連立方程式の文章題(距離) 連立方程式の文章題(増減)
1 次 方程式 解き方
1 次 方程式 解き方- 方程式の解き方かっこがあるときのまとめ 理解したよ! やり方をしっかりと覚えておこう! まず、方程式のかっこをはずす。 そして、いつも通り解くだけ! たったこれだけのことです。 だけど、やっぱりね 普通の方程式よりも計算力は必要一次方程式 1次方程式(小数分数11) 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 1次方程式の解き方(小数,分数1) 名前 次の方程式を解きなさい。 (1) (2) (3) 1 (4) 2 1 (5) 3 NO1 /5 点 3x 1 x 2 2 3 x - + x 1 = 1 x 6 -04 - 2 = +3 6 + = = x 03x+16 - - = x 3 5
1
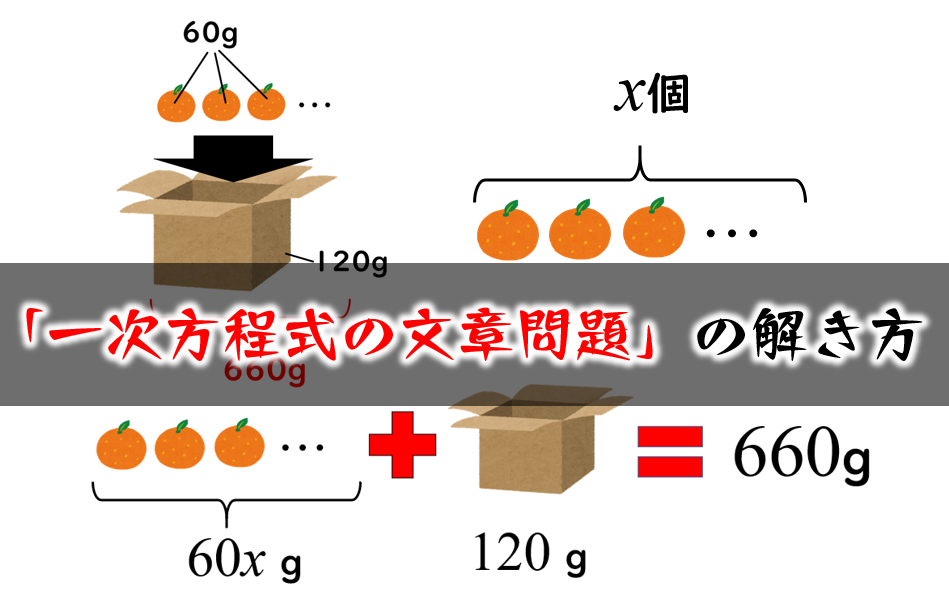
1次不定方程式の整数解の見つけ方と計算方法を , 具体的に問題を解きながらわかりやすく解説していきます 。 全部で5パターンに分けています。 問題集を解く際の参考にしてください! 目次 1 1次不定方程式とは 2 1次不定方程式の種類 3 1次不定方程式の整数解の見つけ方 4 自力で探す 41 自力で探す① 42 自力で探す② 5 互除法で探す 51 (大) (小) (基本パターン) 52 (小) (大) (大小が逆)それは「等式の性質」と「四則計算」「分配法則」「分配法則の逆」「1次式の計算」です。 これらを復讐しながら1次方程式を解いていきましよう。 1方程式を分解する 上の問題の4つの部分①②③④に注目してください。 それぞれ( )と掛け算、わり算でできていて、作業からスタートです。 方法1 ( )をすべて外す⇨四則計算と分配法則! 作業の仕方はい歳 と表すことができます。 このとき、Aくんの年齢を2倍するとお父さんの年齢と等しくなるのだから このような方程式を完成させることができます。 方程式が完成したら、あとは解いていくだけですね (^^) よって、17年後にお父さんはAくんの2倍の年齢になることが分かりました。 17年後であるから、二人の年齢は Aくん13+17=30歳 お父さん43+17=60歳
1階非斉次線形微分方程式の一般解 y’= (1y)/sinxの解き方 変数分離形 y’= (x^2y^2)/2xyの解き方 同次形 y’=2y/xyの解き方 同次形 dy/dx (3/2) (ya)^ (1/3)=0 の一般解と、それらの解曲線の包絡線である特異解 x=e^2t∫3t^2e^ (2t)dtte^2t∫3te^ (2t)dtの解き方 部分積分1次不定方程式の解き方ないか考えてて、 今回の最強の解き方を あるサイトをヒントに作って(?)みました。 教え方はビジュアルよりなので、 最強の解き方は、 まだまだ改良できるとおもいます。 では、 さっそく紹介していきましょう。 ↓↓ ※画像マシマシです。 見にくいので、 12xy=8 のように 2つの文字を含む1次方程式が 2元1次方程式 で、 2元1次方程式を成り立たせる文字の値の組を 解 という。 2元1次方程式の解は無数にある。 例 2xy=8 の解は x=1,y=6 やx=2,y=4など 連立方程式とは { 7x2y = 5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解とな
1 次 方程式 解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
(%E3%80%80)%E2%97%8F.png) |  | |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 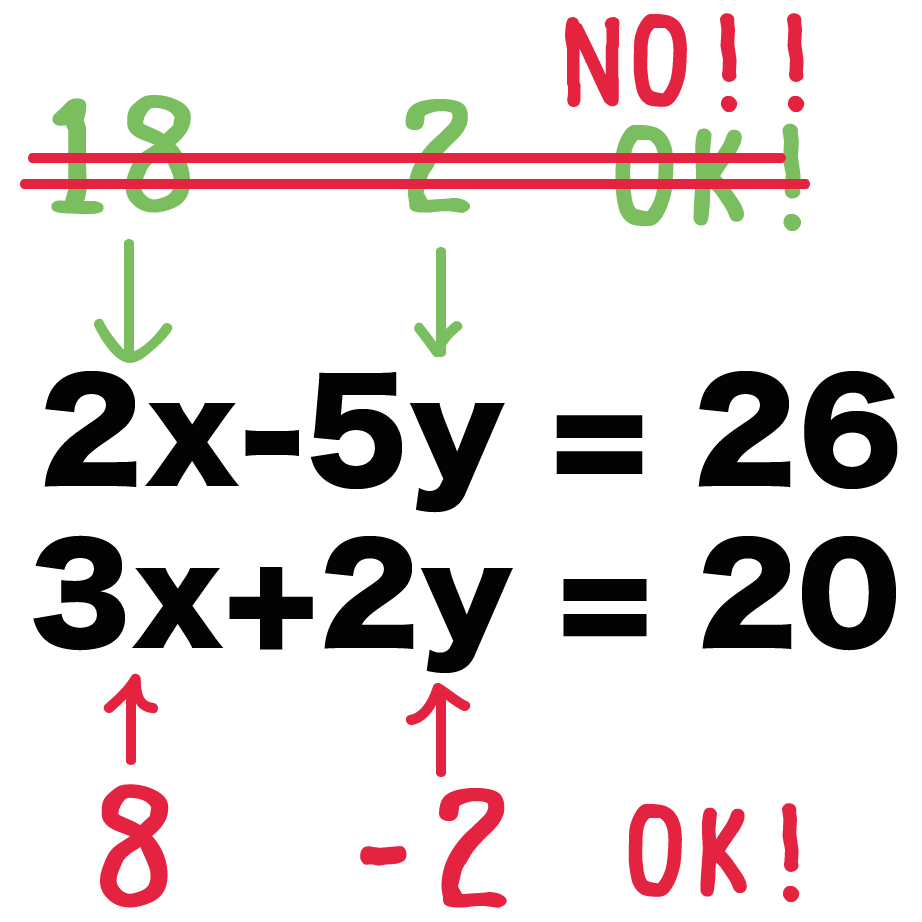 |  |
 |  | |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 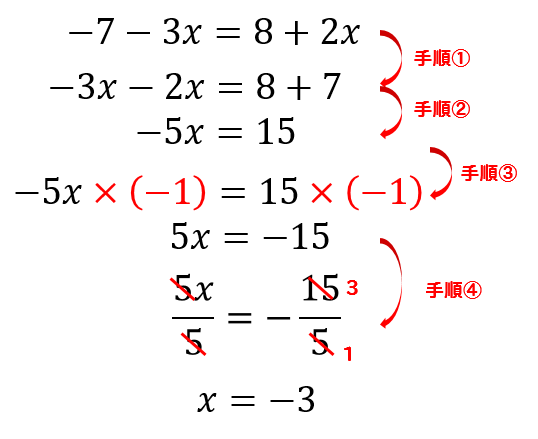 |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「1 次 方程式 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
前、合同式について定義や基本的な定理を示しました。この合同式を使います。もとの方程式2x+3y=1は、 この合同式の両辺を2倍しましょう。 左辺から3xを引きます。mod 3 で考えているのだから好きな辺から好きなだけ3の倍数を引いても相変わらず合同な方程式の必要性や意味、また方程式の中の文字や解の意味を理解し、等式の性質を使って方程式を解く練習、簡単な1次方程式を解く練習ができるプリントです。 方程式の解き方 (1) 答え 方程式の解き方 (2) 答え 方程式の解き方 (3) 答え 方程式
コメント
コメントを投稿